广义表的定义及概念
广义表是线性表的推广,是递归定义的、多层次的线性结构。
广义表的长度定义为最外层包含元素的个数,及最外层逗号数 + 1。
深度定义为所含括弧的重数。(原子的深度为0,空表的深度为1)
任何一个非空广义表都可以分为表头和表尾两部分。
对表头表尾的判断例题如下:

广义表的存储结构
表头表尾分析法
通常采用头、尾指针的链表结构。
结构体定义如下:
1
2
3
4
5
6
7
8
9
10
| typedef enum {ATOM, LIST} ElemTag;
typedef struct GLNode{
ElemTag tag;
union{
AtomType atom;
struct {
struct GLNode * hp, *tp;
}ptr;
};
}*GList;
|
示例如图:
B =(e)
C =(a,(b,c,d))
D = ((),B,C)
E = (a,E)
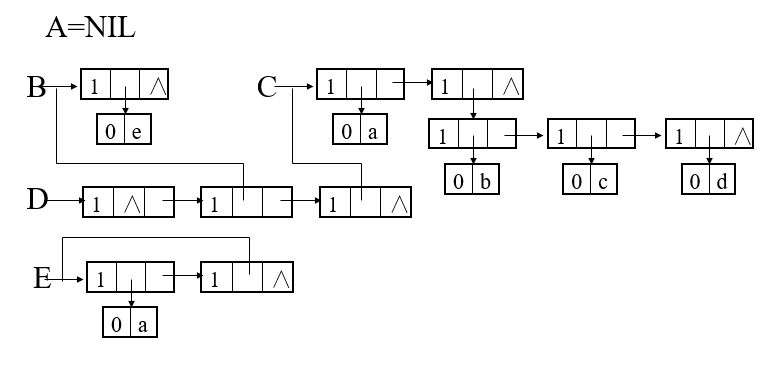
子表分析法
是一种扩展线性链表存储的方式。
结构体定义如下:
1
2
3
4
5
6
7
8
9
10
| typedef enum{ATOM, LIST} ElemTag;
typedef struct GLNode{
ElemTag tag;
union{
AtomType atom;
struct GLNode * hp;
};
struct GLNode * tp;
}*GList;
|
示例如图:
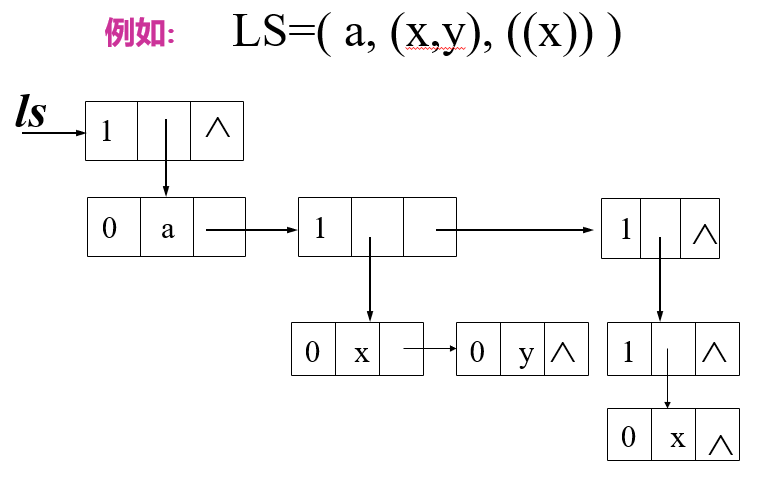
稀疏矩阵的几种表示方法
三元组顺序表
结构体定义如下:
1
2
3
4
5
6
7
8
9
10
| #define MAXSIZE 12500
typedef struct{
int i, j;
ElemType e;
}Triple;
typedef union{
Triple data[MAXSIZE + 1];
int mu, nu, tu;
}TSMatrix;
|
如何求转置矩阵:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void TransposeSMatrix1(TSMatrix M, TSMatrix &T) {
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
if(T.tu){
q = 1;
for(col = 1; col <= M.nu; ++ col)
for(p = 1; p <= M.tu; p ++)
if(M.data[p].j == col){
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
++q;
}
}
return OK;
}
|
先互换行数和列数,以 q 作为新矩阵元素的下标,遍历全部找每一列的元素,这样的做法时间复杂度为O(mu * tu) 。
可以通过确定每一行的第一个非零元在三元组中的位置来更快的计算。
首先用一个数组 num[col] 来记录第 col 列有多少非零元,然后用数组 cpot[col] 来记录在转置后的新矩阵中,非零元的位置。两个数组的计算方法如下:
1
2
3
| cpot[1] = 1;
for(col = 2; col <= M.nu; ++ col)
cpot[col] = cpot[col - 1] + num[col - 1];
|
示例如下:
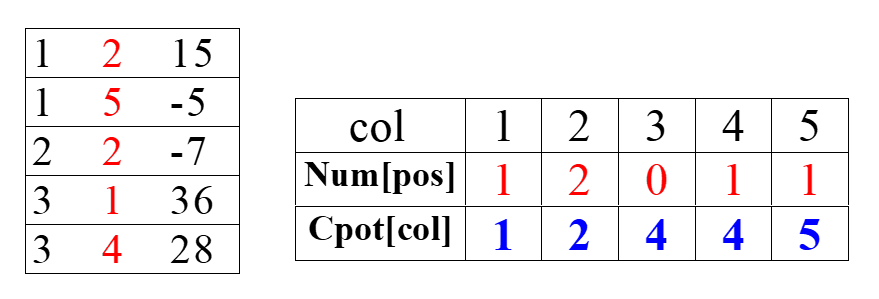
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T){
T.mu = M.nu;
T.nu = M.mu;
T.tu = M.tu;
if (T.tu) {
for (col = 1; col <= M.nu; ++ col)
num[col] = 0;
for (t = 1; t <= M.tu; ++ t)
++num[M.data[t].j];
cpot[1] = 1;
for (col = 2; col <= M.nu; ++ col)
cpot[col] = cpot[col-1] + num[col-1];
for (p = 1; p <= M.tu; ++ p) {
col = M.data[p].j;
T.data[cpot[col]].i = M.data[p].j;
T.data[cpot[col]].j = M.data[p].i;
T.data[cpot[col]].e = M.data[p].e;
++ cpot[col];
}
}
return OK;
}
|
此算法的时间复杂度为O(M.nu + M.tu) 。
行逻辑连接的顺序表
又称为有序的双下标法,其特点是,非零元在表中按行序有序存储,便于进行依行顺序处理的矩阵运算。
结构体定义如下:
1
2
3
4
5
6
| #define MAXMN 500
typedef struct{
Triple data[MAXSIZE + 1];
int rpos[MAXRC + 1];
int mu, nu, tu;
}RLSMatrix;
|
例如:给定一组下标,求矩阵的元素值。(注意要防止跨行)
两个矩阵相乘:
十字链表
对稀疏矩阵的每个非零元,建立一个结点,
结构体定义如下:
向右域right 指向同一行中下一个非零元,向下域down 指向同一列中下一个非零元。
1
2
3
4
5
6
7
8
9
10
11
| typedef struct OLNode{
int i, j;
ElemType e;
struct OLNode *right, *down;
}OLNode,*OLink;
typedef struct {
OLink *rhead, *chead;
int mu, nu, tu;
} CrossList;
|
创建稀疏矩阵,采用十字链表存储表示:

