内部排序简介

内部排序的过程是一个逐步扩大记录的有序序列长度的过程。

待排记录的数据类型定义如下：

#define MAXSIZE  1000 // 待排顺序表最大长度
typedef int KeyType;  // 关键字类型为整数类型

typedef struct {
    KeyType key;             // 关键字项
    InfoType otherinfo;      // 其它数据项
} RcdType;                   // 记录类型

typedef struct {
    RcdType r[MAXSIZE+1]; // r[0]闲置
    int length;           // 顺序表长度
} SqList;                 // 顺序表类型

希尔排序（插入排序）

插入排序：将无序子序列中的一个或几个记录“插入”到有序序列中，从而增加记录的有序子序列的长度。

希尔排序基本思想：对待排记录序列先做宏观调整（跳跃式的插入排序），再做微观调整。

具体做法为：将记录序列分成若干子序列，分别对每个子序列进行插入排序。待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

举例如图：

希尔排序的过程

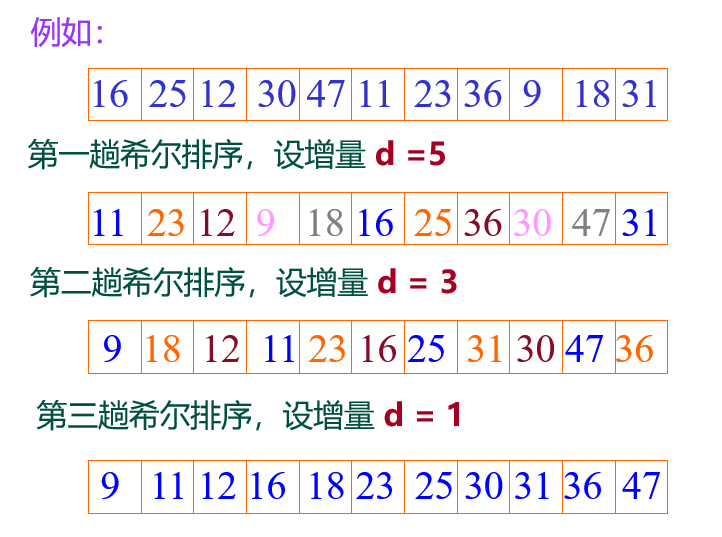
希尔排序例题

代码如下：

// 一趟排序，在每个分段内做选择排序
void ShellInsert ( SqList &L, int dk ) {
    for (i = dk + 1; i <= n; ++ i)
        if (L.r[i].key < L.r[i-dk].key) {
        	L.r[0] = L.r[i];            // 暂存在R[0]
        	for (j = i - dk; j > 0 && (L.r[0].key < L.r[j].key); j -= dk)
           		L.r[j + dk] = L.r[j];  // 记录后移，查找插入位置
        	L.r[j + dk] = L.r[0];                // 插入
      	} // if
} // ShellInsert

void ShellSort (SqList &L, int dlta[], int t){    // 增量为dlta[0..t-1]对顺序表L作希尔排序
     for (k = 0; k < t; ++ k)
         ShellInsert(L, dlta[k]); //一趟增量为dlta[k]的插入排序
} // ShellSort

注意：增量序列可以有各种取法，但是应使增量序列中的值没有除 1 之外的公因子，并且最后一个增量值必须等于1。

快速排序

起泡排序

快速排序

代码如下：

int Partition (RedType R[], int low, int high) {
	R[0] = R[low];  
    pivotkey = R[low].key;  // 枢轴
    while (low<high) {//从表的两端交替地向中间扫描
		while(low<high&& R[high].key>=pivotkey)
        	-- high;      //将比枢轴记录小的记录交换到低端
        R[low] = R[high];
		while (low<high && R[low].key<=pivotkey) 
            ++ low;      //将比枢轴记录大的记录交换到高端
        R[high] = R[low];
    }
    R[low] = R[0];     
    return low；//枢轴记录到位，返回
}// Partition                                     //枢轴位置

void QSort (RedType & R[], int low, int high ) {
  // 对记录序列R[low..high]进行快速排序
	if (low < high) {             // 长度大于1   
    	pivotloc = Partition(R, low, high);// 对 R[s..t] 进行一次划分
    	QSort(R, low, pivotloc-1);
      	// 对低子序列递归排序，pivotloc是枢轴位置
        QSort(R, pivotloc+1, high); // 对高子序列递归排序
   	}
} // QSort

void QuickSort( SqList & L) {
    // 对顺序表进行快速排序
	QSort(L.r, 1, L.length);
} // QuickSort

快速排序的平均时间为 $T_{avg}=kn\ln n$ ，其中 n 为待排序列中记录的个数，k 为某个常数。经验证明，在所有同数量级的此类排序方法中，快排的 k 最小，因此快排最好。

快排的时间复杂度为 $O(n\log n)$

若待排记录的初始状态为按关键字有序时，快排将退化为起泡排序，其时间复杂度为 $O(n^2)$ 。为了避免出现这种情况，需要在进行一次划分之前进行预处理（三者取中），即先对 $R(s).key$ ，$R(t).key$ 和 $R(\lfloor (s+t)/2\rfloor) .key $ 进行相互比较，然后取关键字为“三者之中”的记录为枢轴记录。

选择排序

堆排序

将保存的数列视作完全二叉树，则树中所有非终端结点的值均不大于（不小于）其左右孩子结点的值。

堆顶元素取最大值 == 根结点取最大值 == 大顶堆

堆顶元素取最小值 == 根结点取最小值 == 小顶堆