平衡二叉树
是二叉排序树的另一种形式。
特点:树中每个结点的左右子树深度之差的绝对值不大于一。
调平
构造
在插入过程中,采用平衡旋转技术。
四种情况:
LL型
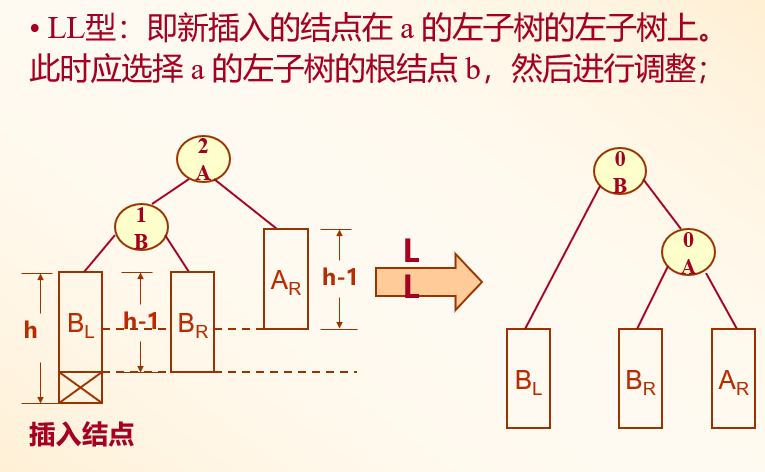
RR型
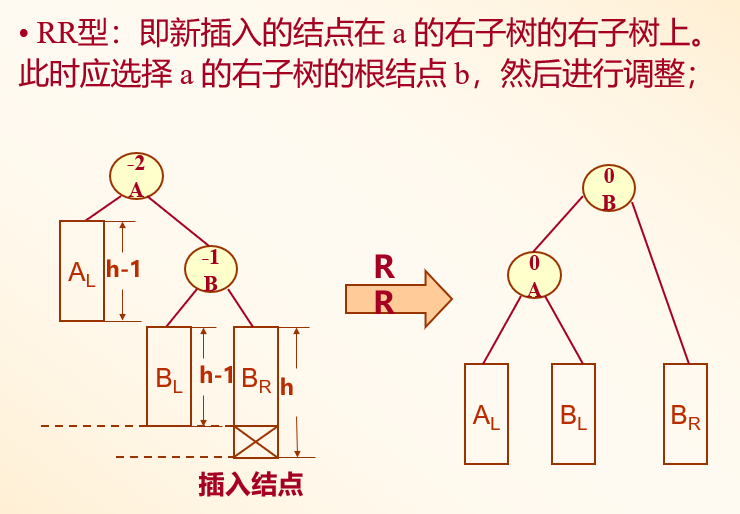
LR型
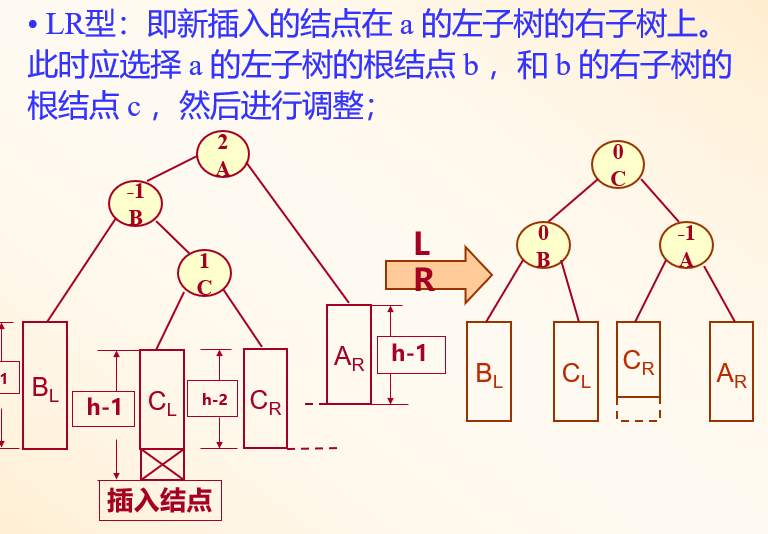
RL型
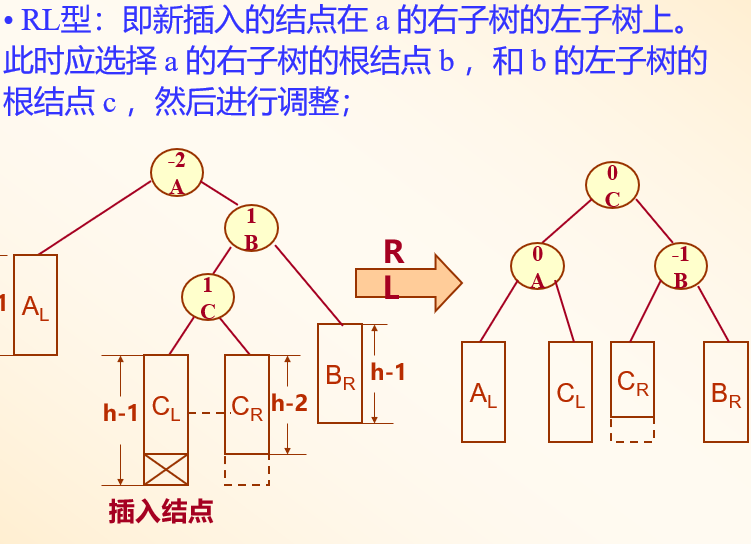
B- 树的定义
是一种平衡的多路查找树。
一棵 m 阶的 B- 树,或为空树,或为满足下列特性的 m 叉树。
所有非叶节点均至少含有 $\lceil m/2\rceil$ 棵子树,至多含有 m 棵子树
根结点或为叶子结点,或至少含有两棵子树
所有非终端结点含有下列信息数据
$n,A_0,K_1,A_1,K_2,A_2…K_n,A_n$
其中,$K_i$ 是关键字,且均从小到大有序排列,$A_i$ 是指向子树根结点的指针,且指针$A_{i-1}$ 所指子树上所有关键字均小于$K_i$ ,$A_n$ 所指子树上所有关键字均大于 $K_n$
树中所有叶子结点均不带信息,且在树中的同一层次上(实际上这些结点不存在,只想这些结点的指针为空)
哈希表
定义
哈希函数:关键字与表中存储位置之间建立的函数关系。
哈希函数容易产生冲突:
- 即$key1\ne key2 而 f(key1)=f(key2)$ 。具有相同函数值的关键字对该哈希函数来说称作同义词。
- 很难找到一个不产生冲突的哈希函数,一般情况下只能选择恰当的哈希函数,使冲突尽可能少。
因此在找到一个“好”的哈希函数的同时,也要找到一种“处理冲突”的方法。
根据设定的哈希函数,和选中的处理冲突方法,将一组关键字映像到一个有限的、地址连续的地址集上,并以关键字在地址集中的“象”作为相应记录在表中的存储位置,如此构造所得的查找表称之为哈希表。
构造方法
对数字的关键字有以下几种构造方法;非数字的可以先进行数字化处理。
直接定址法
哈希函数为关键字的线性函数
适用于 地址集合的大小 == 关键字集合的大小
数字分析法
平方取中法
折叠法
除留余数法
随机数法
处理冲突的方法
实际含义:为产生冲突的地址寻找下一个哈希地址。通常有如下几种方法。
开放地址法
为产生冲突的地址 $H(key)$ 求得一个地址序列:$H_0,H_1,…,H_S (1\le s\le m-1)$
其中:$H_0=H(key),H_i = (H(key)+d_i)mod m (i=1,2,…,s)$ m 为哈希表长
对于增量 $d_i$ 有三种取法:
线性探测再散列
$d_i=1,2,3,…,m-1$
在处理同义词的冲突过程中又添加了非同义词的冲突,称为二次聚集
可以覆盖哈希表中所有地址
二次探测再散列
$d_i=1^2,-1^2,2^2,-2^2$
表长 m 必须为形如 $4j+3$ 的素数时,才能覆盖所有地址
伪随机探测再散列
$d_i$ 是一组伪随机数列,或者 $d_i=i\times H_2(key)$ (又称双散列函数探测)
是否能够覆盖取决于伪随机数列(m和di没有公因子)
再哈希法
$H_i=RH_i(key) i=1,2,…,k$
$RH_i$ 均是不同的哈希函数,即在同义词产生地址冲突时,计算另一个哈希函数地址,直到冲突不再发生。这种方法不易产生“聚集”,但增加了计算的时间。
链地址法
将所有哈希地址相同的记录都链接在同一线性链表中。(同一链表中关键字自小到大有序)
建立一个公共溢出区
一旦发生冲突,都填入溢出表。

