状态树
账户地址的大小是160bits,表示为40个16进制数
需要实现从地址到状态的映射,考虑以下几个需求:
- 易于查找
- 能够提供保证数据正确的证明
- 账户地址数量多
- 不能随着每次出块全部发布出去(每次交易少,状态变化少,出块时间短)
- 是否需要规定存放顺序?
Trie 字典树,前缀树
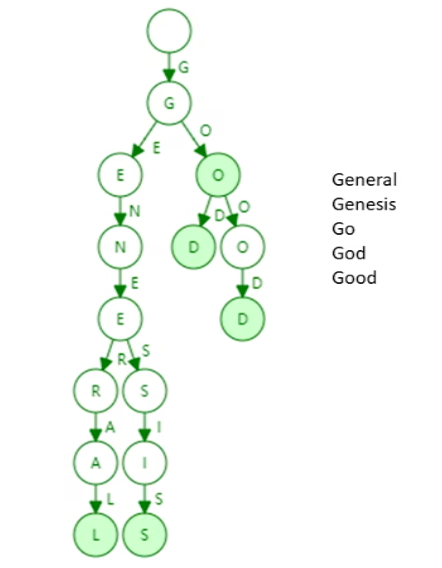
用于存储key-value,有以下优点:
- 输入不变,构成的trie是同一棵树,不需要考虑顺序问题
- 每个结点的分支数目取决于key的取值范围,因此以太坊帐户的分支为17个(0~f以及一个结束位)
- 查找需要的时间取决于key的长度,长度越长,需要访问内存的次数越多
- 不可能出现哈希碰撞(如果用哈希表来存可能会有这个问题)
- 更新的局部性,当需要修改value时,方便查找,不需要遍历整棵树
有以下缺点:
- 如上图,下部ral和sis都是单支,造成了存储空间的浪费
Patricia Tree 压缩前缀树
进行路径压缩后的前缀树
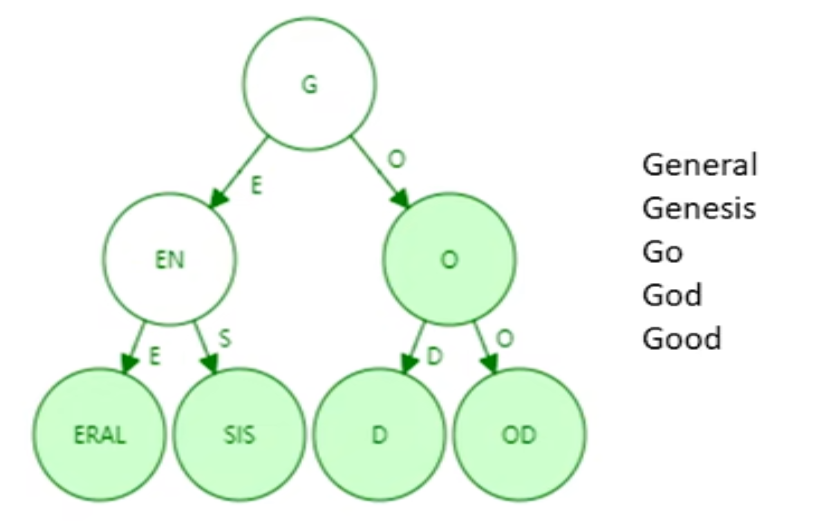
加入新key,路径可能需要扩展开来
键的取值比较稀疏时,压缩效果较好
以太坊的账户地址很长,为$2^{160}$,可以有效避免账户冲突,导致取值稀疏
Merkle Patricia Tree
把普通指针替换为哈希指针
带来的好处:
- 不被篡改
- 能够证明数据的正确性
- 可以证明某个帐户不在tree上
Modified MPT
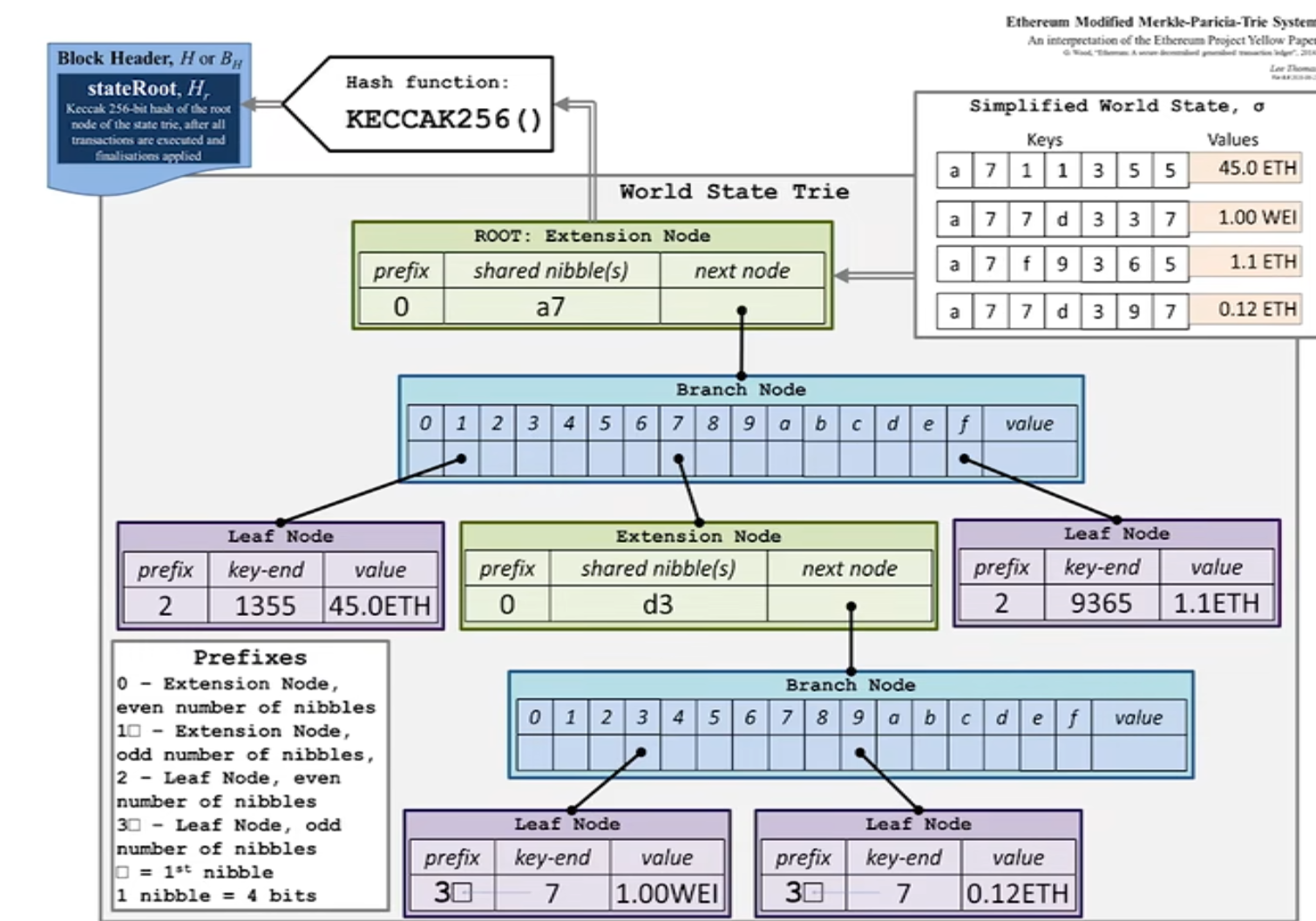
实际上,每个合约帐户自己也形成一个MPT(storage),因此总体结构是一颗大的MPT包含着很多小的MPT
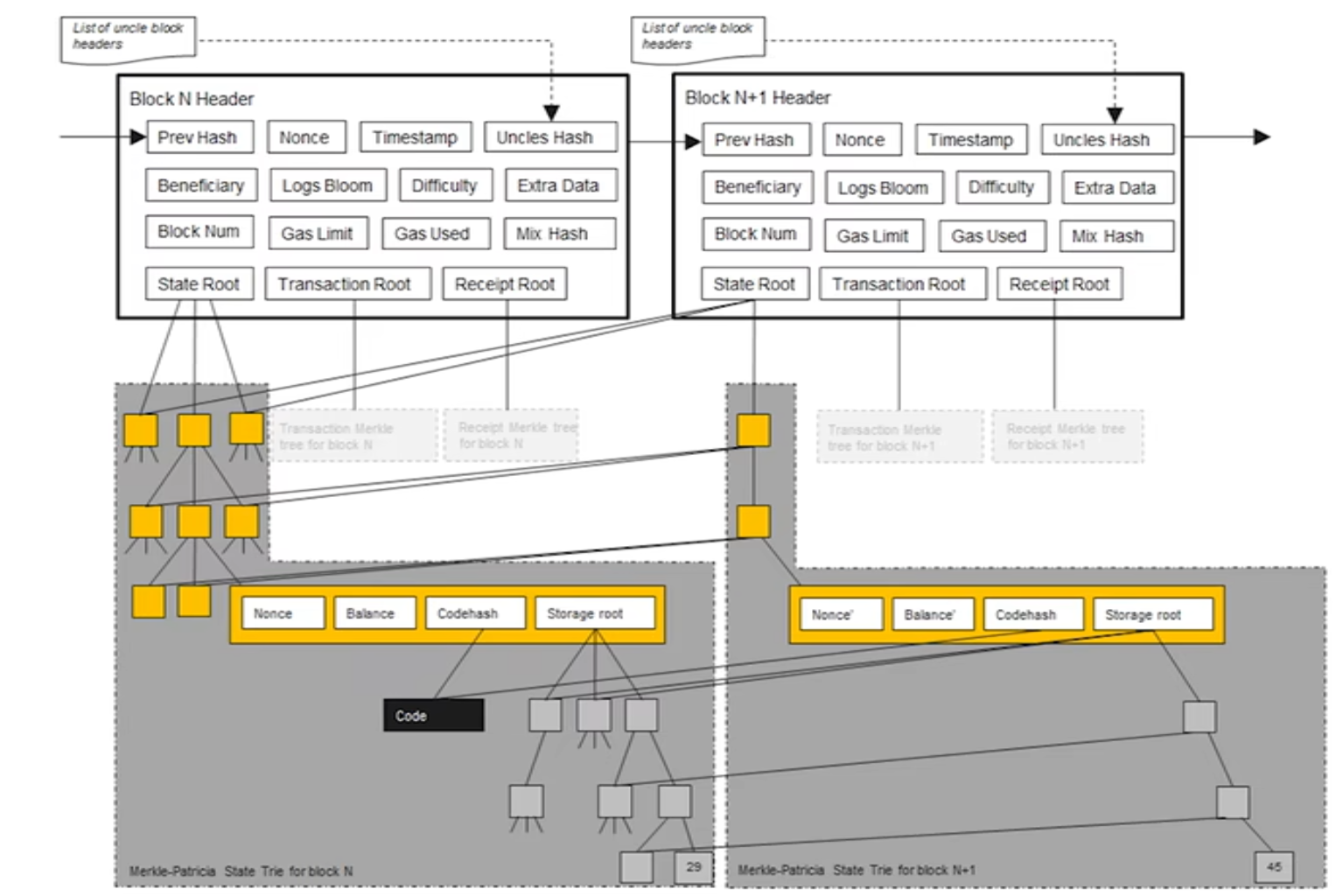
如图所示,是N+1块在合约账户中改变了一个存储值(29->45)时,state root的变化和每个节点指针的指向情况
保留历史状态的原因:可能需要状态回滚(出现分叉后交易undo),与比特币简单的交易脚本不同,以太坊中有比较复杂的智能合约代码,如果这些合约改变了账户状态,很难根据改变后的状态和合约代码推断之前的状态,因此需要保存历史状态,方便回滚。
帐户状态的存储
需要经过序列化处理(将对象的状态信息转换为可以存储或传输的形式的过程)
RLP:Recursive Length Prefix
在以太坊中,采用了一种名为Recursive Length Prefix(RLP)的方法对交易、账号、合约等基础的数据结构进行序列化处理,从而实现对链上数据的网络传输和持久化存储。
交易树
MPT结构
可以用于提供merkle proof
收据树
MPT结构,为了便于智能合约的执行
可以用于提供merkle proof
Bloom Filter
用于查找一个元素是否在集合中
每个交易完成后形成一个收据,收据中包含着一个Bloom Filter
块中所有收据的Bloom Filter组成一个大的Bloom Filter,保存在块头中
查询时先使用块头中的Bloom Filter定位到具体区块,再进行进一步查找
算法描述
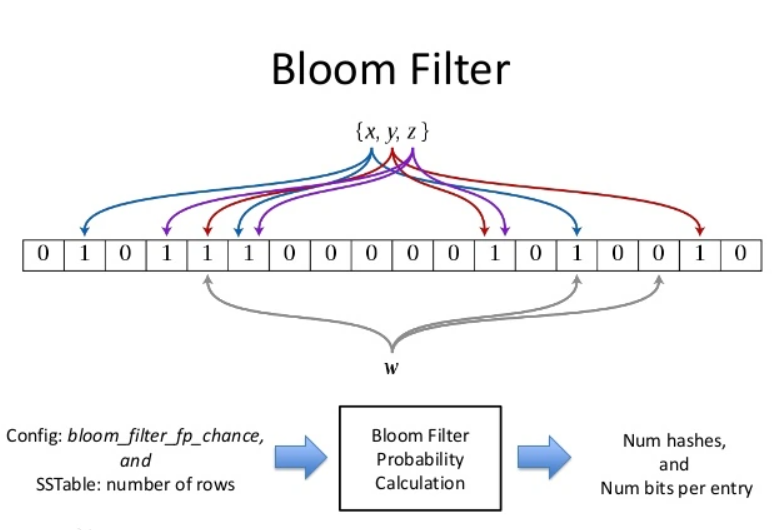
bloom filter是一个有m bits的bit array,每一个bit位都初始化为0。并且定义有k个不同的hash function,每个都以均匀的随机分布将元素hash到m个不同位置中的一个。n为要添加到bloomfilter里面的元素。p为错误率。所以相关的参数为:m n k p
如果检测结果为是,该元素不一定在集合中;但如果检测结果为否,该元素一定不在集合中。
增删查改操作
添加过程:首先,用k个hash function将它hash得到bloom filter中k个bit位,之后将这k个bit位置1
查询过程:即判断它是否在集合中,用k个hash function将它hash得到k个bit位。若这k bits全为1,则此元素可能在集合中;若其中任一位不为1,则此元素比不在集合中
删除过程:不允许remove元素,因为那样的话会把相应的k个bits位置为0,而其中很有可能有其他元素对应的位。因此remove会引入false negative,这是绝对不被允许的。
修改过程:删除都不允许了,修改更不允许

