TBST:Threaded Binary Search Tree
线索二叉树
当我们创建二叉树时我们会发现其中一共有两个指针域,有的指针域指向的结构为空,这也就浪费了很多空间。此时可以利用那些空地址,存放指向结点在某种遍历次序之下的前驱和后继结点的地址。
由于它充分利用了空指针域的空间(这等于节省了空间),又保证了创建时的一次遍历就可以 终生享用前驱后继的信息(这意味着节省了时间)。所以在实际问题中,如果所用的二叉树经常要遍历或查找结点时需要某种遍历序列中的前驱后继,那么采用线索二叉链表的存储结构就是非常不错的选择。
AVL Tree
二叉平衡查找树,其查找、删除和插入的时间复杂度为$O(\log n)$,添加仅需$O(1)$次旋转调整、删除最多需要 $O(\log n)$次旋转调整
在二叉树的基础上加入平衡的特点,即要求每个结点的左右子树高度差不超过1,这样做可以降低树的高度,从而减小平均搜索长度
使用平衡因子来限制左右子树的高度差不能超过1
平衡树、线索二叉树与区块链查询的结合
线索二叉树+平衡树
以时间戳作为关键字来检索
插入:
- 时间戳总是增大,因此新的节点总是放在右边(需要进行RR操作)
- 感觉是不是有点点浪费时间
查找:
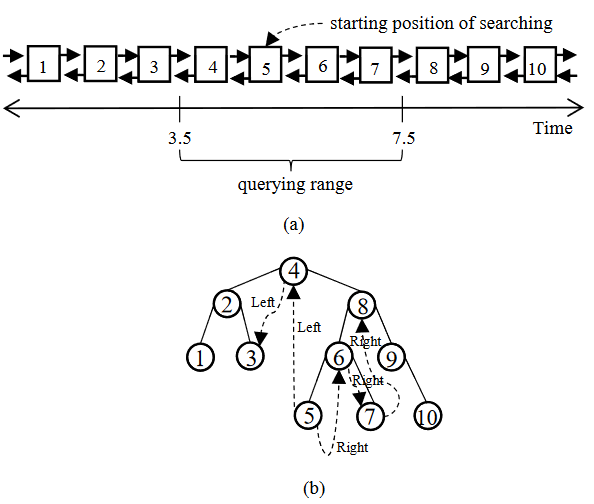
- 需要遍历查询4-7号块中的交易数据:先二分,再从二分的节点开始遍历
RBTree
不严格的二叉平衡查找树,维持平衡的同时不需要花费太多时间,其查找、删除和插入的时间复杂度为$O(\log n)$,添加、删除都仅需$O(1)$次旋转调整
特征如下
节点是红色or黑色
根节点是黑色的
每个叶子节点都是黑色的空节点,也就是说,叶子节点不存储数据
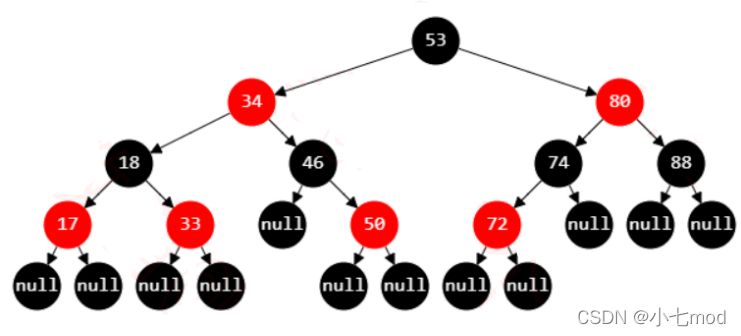
任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的
每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点
由于一个节点到叶子节点的路径为全黑节点或红黑交替节点,而要求两种路径黑色节点数相同,因此最长路径是红黑交替节点,最短路径是全黑节点,红黑树保证最长路径不超过最短路径的二倍,因而近似平衡
红黑树的平衡
弱平衡、黑高度平衡
使用红黑树的5条性质证明红黑树等价于4阶B-树:将所有红色节点上移到黑色父节点,形成一颗4阶B-树
红黑树与区块链查询的结合
MRB Tree:红黑树和默克尔树结合
在默克尔树的基础上,向中间节点添加一个key用于检索交易,按照红黑树的性质进行插入
插入:
- 此处疑问:论文中的插入情况违背了红黑树的平衡规则
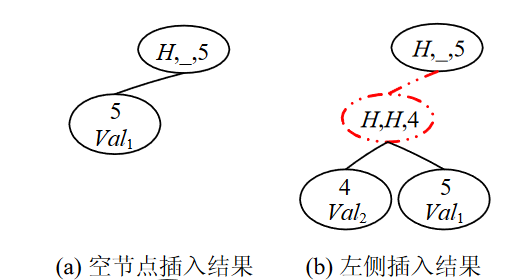
查询算法:
- 给定交易关键字key,首先在内存区块中检索
- 不在内存区块中,加载数据库中上一区块的MRBTreeIndex,开始在区块中查找
- 小于等于则在左子树,否则在右子树,都不存在则不在当前区块中
B-Tree
多路平衡查找树
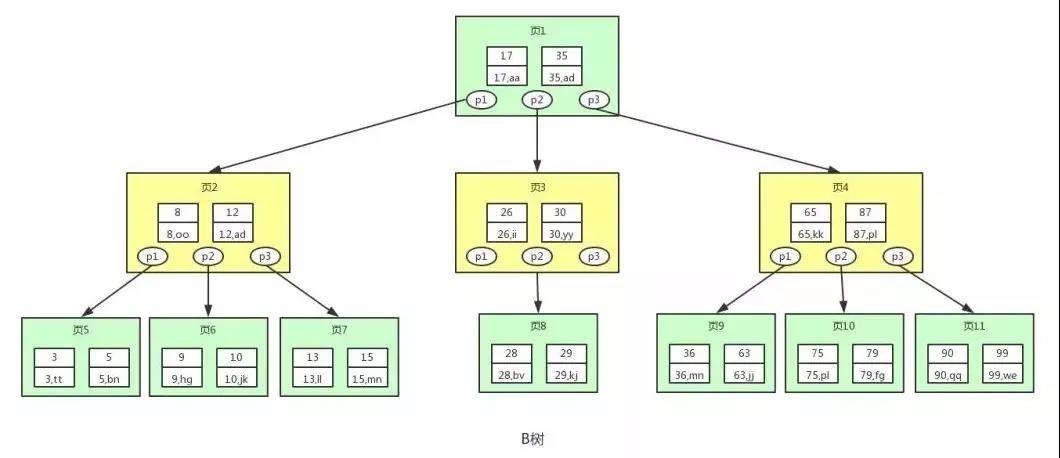
一个m阶B-树是满足以下特征的m叉树:
- 根节点至少有两个子女
- 每个中间节点都包含k-1个元素和k个孩子,其中$\frac{m}{2}\le k \le m$
- 每个叶子节点都包含k-1个元素,其中$\frac{m}{2}\le k \le m$
- 所有的叶子节点都位于同一层
- 每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划
主要应用于文件系统以及数据库索引
B+Tree
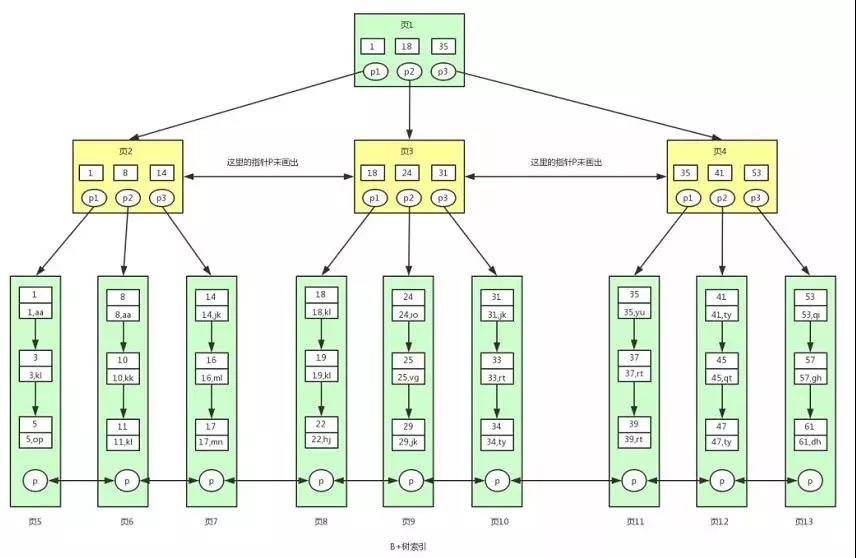
一个m阶B+树是满足以下特征的m叉树:
- 非叶子节点不存储数据,只用作索引
- 有k个子树的中间节点包含有k个元素(B树中是k-1个元素)
- 所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素
- 另外,同一层的节点之间形成双向链表,叶子节点中的数据形成单向链表
B+树 vs B-树的优势:
- 单一节点存储更多的元素,使得查询的IO次数更少(树更矮胖)
- 所有查询都要查找到叶子节点,查询性能稳定
- 所有叶子节点形成有序链表,便于范围查询、分组查询等等

