论文主要贡献
vChain框架:减轻用户的存储和查询计算成本,并使用可验证的查询来保证结果的完整性
基于累加器的可验证数据结构(ADS: authenticated data structure):支持对任意查询属性进行动态聚合,实现可验证布尔范围查询
两个索引:聚合块间和块内的数据,提供高效查询和验证
- 倒排前缀树结构:加速大量订阅查询的处理
Introduction
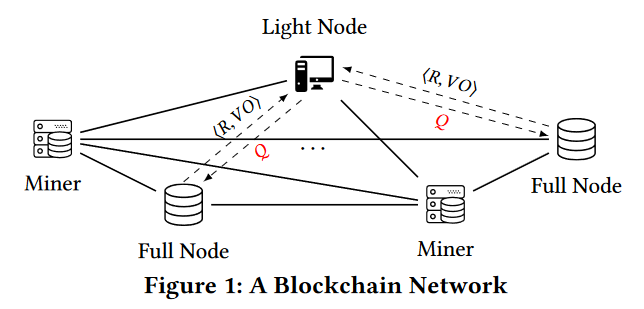
分为全节点(普通全节点和挖矿节点)和轻节点。轻节点向全节点发送查询请求Q,全节点向轻节点提供查询结果集合R和验证对象VO(verification object),其中VO是由SP构造的用于让轻节点验证查询结果的完整性和健全性的验证对象。
ADS数据结构由现有的外包数据库可验证查询技术而来,进行的变化和调整如下:
不可篡改性:
- 外包数据库:由数据所有者私钥签名来保障
- 区块链:不存在数据所有者
数据集合大小:
- 外包数据库:数据集合大小有限
- 区块链:数据量无限大
生成:
- 外包数据库:需要即可创建生成
- 区块链:由于数据存储的持久性,需要一个万能的ADS来满足查询需求
问题描述及模型
模型描述
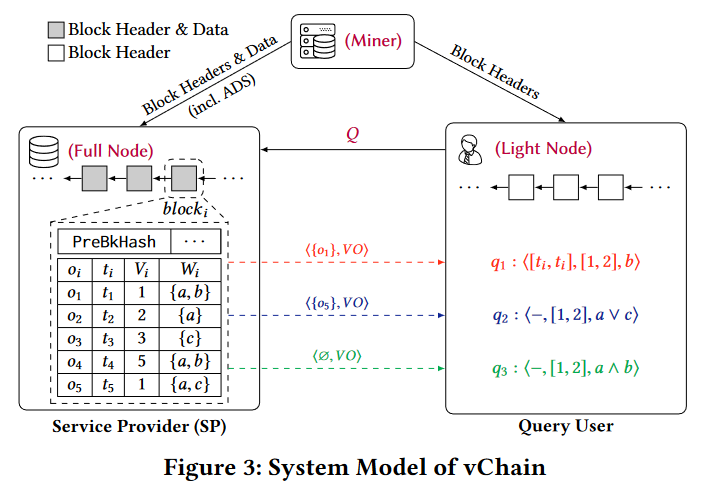
区块链中保存的数据看作一个集合 $\{o_1,o_2,…,o_n\}$,其中 $o_i=
针对两种布尔范围查询
时间序列窗口查询
用户搜索在某个时间段内出现的记录
一条查询可以表示如下
其中 $t_s t_e$ 分别是时间段的开始和结束时间,$[\alpha, \beta]$ 表示数字属性的多维范围选择谓词(人话:n个属性值的数值范围),$\Upsilon$ 表示集值属性值的单调布尔函数,可以看作是一个合取范式
返回 $O$ 要满足 $\{o_i = ⟨t_i,V_i,W_i⟩ | t_i \in [t_s, t_e]\land Vi \in [\alpha, \beta] \land \Upsilon(W_i) = 1\}$
订阅查询
用户注册自己感兴趣的查询内容,SP为用户提供结果(新块确认完成后推送新信息以及验证对象)
一条查询可以表示如下
SP持续返回查询结果 $O$ 直到查询被用户取消,满足 $\{o_i = ⟨t_i,V_i,W_i⟩ | Vi \in [\alpha, \beta] \land \Upsilon(W_i) = 1\}$
需要解决的问题:SP不可信
解决方法:让SP证明查询结果的完整性。
在查询处理过程中,让SP检查嵌入在链上的ADS,构建一个VO,包含结果的验证信息。VO连同结果一起返回给user。user可以利用VO确定查询结果的正确性和完整性。
密码学知识
哈希加密函数,双线性配对(Bilinear Pairing),多重集(Multiset),加密多重集累加器。
加密多重集累加器
一个函数acc(·),以抗碰撞方式将多重集映射到循环乘法群中
基本解决方案
选择传统的MHT作为ADS的缺点:
- 为了支持涉及任意属性集的查询,需要为每个块构造指数数量的MHT
- 不适用于集值属性
- 不同块的MHT无法有效聚合,使其无法进行块间优化
为了克服这些缺点,提出了基于新的基于累加器的ADS方案的新型身份验证技术,该方案将数值属性转换为集值属性,并支持对任意查询属性进行动态聚合。
ADS的生成
在区块中加入新属性AttDigest,用ObjectHash来表示原来的MerkleRoot
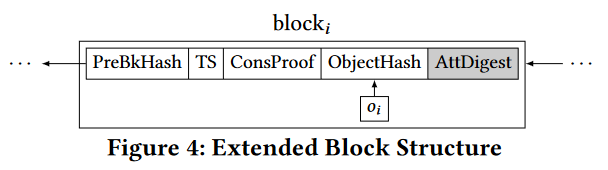
使用多重集累加器作为AttDigest:
集值属性布尔查询的可验证查询过程
查询条件$“Sedan” \land (“Benz” \vee “BMW”)$
SP可以应用$ProveDisjoint(\{“Van “,” Benz”\},\{ “ Sedan “ \},pk)$ 生成一个不相交的证明$\pi$作为不匹配对象的VO(验证对象)。
相应地,用户可以从区块头中检索$AttDigest_i= acc(\{“Van”,“Benz”\})$,并使用$VerifyDisjoint(AttDigesti,acc(\{“Sedan”\}),π,pk)$来验证不匹配。
多重集累加器的结构
基于双线性配对和q-SDH假设
公钥长度和最大多重集的大小成线性关系
基于双线性配对和q-DHE假设
允许聚合多个累加值或多个不相交的证明
公钥长度和系统中可能的最大属性值的大小成线性关系
扩展到范围查询
需要将数值属性转化为集值属性:
将数值改为二进制后再改为前缀集合
- 例如4表示为$trans(4)=\{1,10,100\}$,*为通配符
- 向量 $(4,2)$ 表示为 $\{1∗_1, 10∗_1, 100_1, 0∗_2, 01∗_2, 010_2\}$
将范围查询条件转化为布尔查询
$[0,6]$ 转化为 $\{ 0 \vee 10 \vee 110 \}$
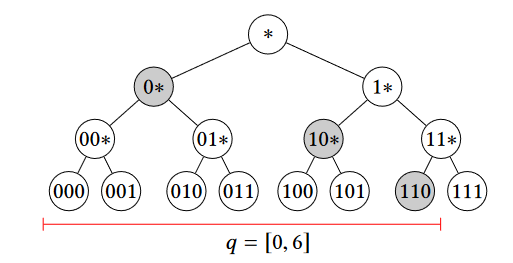
查找某个取值是否在查找范围内:判断二者交集是否为空,为空即不在范围内
批量验证
块内索引
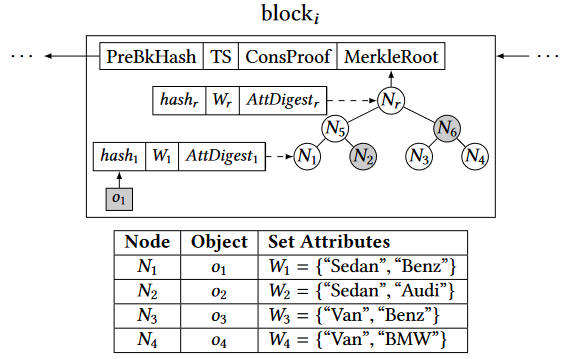
最大化每个节点下对象的相似性:计算Jaccard相似系数,在构造Merkle Tree时将较为相似的节点作为左右叶子节点进行结合,构造一棵二叉平衡树
非叶子节点的各个属性值赋值如下:
- $W_n=W_{nl}\cup W_{nr}$
- $AttDigest_n=acc(W_n)$
- $hash_n=hash(hash(hash_{nl}|hash_{nr})|AttDigest_n)$
块间索引

使用跳表,其搜索、删除和添加的平均时间复杂度是$O(logn)$
按照指数来建立索引
在块属性中添加$SkipListRoot$用于保存块间索引内容:
$SkipListRoot=hash(hash_{L_{2}}|hash_{L_{4}}|hash_{L_{8}}|…)$
$hash_{L_{k}}=hash(PreSkippedHash_{L_{k}}|AttDigest_{L_{k}})$
$AttDigest_{L_k}= acc(W_{L_k})$
$W_{L_k}=\sum^i_{j=i-k+1}W_j$
在线批量验证
使用累加器construction2中的sum函数,将以相同理由mismatch的结果聚合起来

可验证订阅查询
由查询用户注册,并持续处理,直到取消注册为止。当SP看到新确认的区块时,需要将结果与VO一起发布给注册用户。
主要难点在于,需要在新的区块到达后同时进行大量的查询,生成很多结果。此时为了节约查询的时间,可以暂时推迟数据的不匹配验证。
索引
查询处理的主要开销来自SP对不匹配对象的证明的生成
不同的订阅查询可能有相同的不匹配原因,这类查询可以共享不匹配证明
结构
使用倒排前缀树结构:TP-Tree,由以下部分组成
- 前缀树结构
- 倒排文件:前缀树的每个节点都与一个倒排文件相关联,该文件是基于该节点下索引的订阅查询而构建的
- 数值范围文件RCIF(Range Condition Inverted File),用于查询数值范围是否匹配,包含以下内容
- 查询q
- 覆盖类型:q全部/部分 覆盖了所有节点的数值范围$S$
- 布尔函数文件BCIF(Boolean Condition Inverted File),只记录全部覆盖了节点空间的查询,用于检查布尔集合是否匹配,包含以下内容
- 查询条件集合
- 相对应的查询q
- 数值范围文件RCIF(Range Condition Inverted File),用于查询数值范围是否匹配,包含以下内容
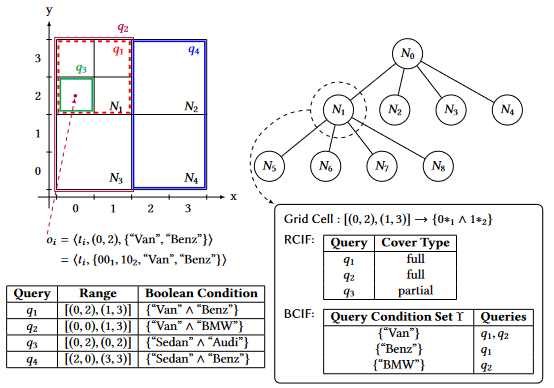
IP-Tree由SP自上而下的构建:
- 创建根节点,把所有查询作为部分覆盖加入节点
- 将根节点拆分成四个等大的子结点
- 对于子结点:
- 如果某个数值范围查询部分或全部覆盖了节点空间,则加入到RCIF中
- 如果某个布尔集合全部覆盖了该结点的空间,则加入到BCIF中
- 出现部分覆盖的情况时,进一步拆分当前结点
- 当所有叶子节点中都没有部分覆盖的查询时,不需要再拆分节点
- 注意当树变得过于深,超过某一个给定阈值后,将会变成没有TP-Tree的情况
查询过程
查询—>树的遍历
当新的数据对象o被添加后:
从根节点开始自上而下开始遍历
到达节点$n_q$后:
- 如果RCIF中的某条查询范围达到了全覆盖
- 符合BCIF中的查询条件,则将对象o添加到该查询的结果中
- 不符合BCIF中的查询条件,则调用ProveDisjoint(·)函数并且将不匹配证明添加到结果中
- 如果RCIF中的某条查询范围是部分覆盖
- 什么都不做
- 如果RCIF中的某条查询范围达到了全覆盖
将订阅查询的索引扩展到块内索引
依然以之前的查询过程进行查询,但是需要一直遍历到叶子节点
延迟验证
延迟不匹配的验证以减少查询验证的成本
采取的做法:当有符合条件的结果时,或距离上次返回结果已经过了一段时间(阈值)时,返回不匹配结果。此时VO应该证明当前数据对象是匹配的,并且该结果和上一次结果之间的所有查询都不匹配
如果等待有结果产生后再使用时间窗口查询生成证明,会造成:无法共享不匹配证明;用户将需要同时验证很多证明。
因此使用块间索引来生成不匹配证明。但是新块还不可用,不知道未来的数据对象是否共享同一个不匹配证明
使用一个栈来保存不匹配的块。首先找到跳表的最大跳过距离$L_i$,其中跳过的块覆盖了栈顶的m个元素,区块的AttDigest被替代为$AttDigest_{L_i}$,使用ProofSum函数来聚合不匹配证明,这样当找到匹配结果后,SP不需要从头聚合不匹配证明。

