Introduction
传统区块链系统:只能进行键值对查询,不能进行范围查询
实现可验证范围查询:
区块链中的写入操作需要的gas费远远高于读取操作
- 通过智能合约建立ADS结构,但是如果使用Merkle Tree作为ADS结构,gas费用会很高
- 插入新节点引起叶子节点更新(为了有序)
- 插入新节点引起所有父结点hash值改变
- 插入新节点引起递归性的节点分裂
本文贡献:
首次讨论了混合存储的区块链系统中,可验证范围查询的问题
提出一种新的ADS结构,叫做Gas-Efficient Merkle Merge Tree($GEM^2-tree$)
- 将写入操作转化为读取和计算操作
- 不再维护一整颗树,而是维护多颗小树
- 减小更新费用(?)
优化后的ADS称为$GEM^{2*}-tree$,进一步减小维护数据需要的费用
- 实验证明
Problem Formulation
系统模型
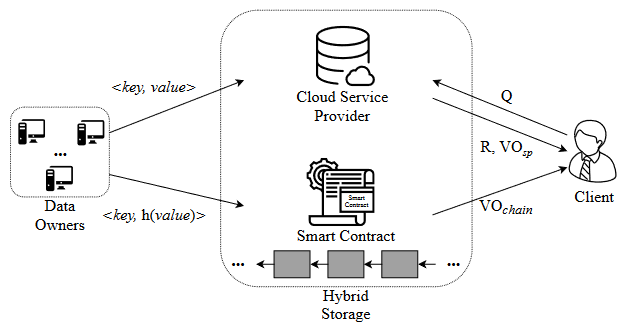
ADS保存于智能合约和SP中
Baseline Solutions
MB-Tree
当需要插入一个新数据对象时:(F叉树,N个叶子节点即N个数据对象)
- 首先找到用来存放该对象的叶子节点位置,需要的gas费用为$\log_FN\cdot C_{sload}$
插入节点需要额外的gas费用$C_{sstore}$
更新父结点的所有哈希值:共有$\log_FN$个父结点。每个节点需要的gas费为$F\cdot C_{sload}+C_{hash}+C_{supdate}$
最坏情况下需要产生$O(log_FN)$个
节点的分裂,每个节点需要$2C_{sstore}$的gas来存储数据(分裂成两个),以及$F\cdot C_{sload}+C_{supdate}$ 的加载和更新费用
总的gas是
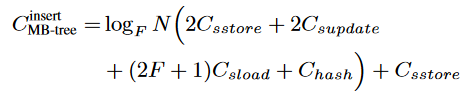
可以看出,N的大小与增加的gas费成对数关系
需要关注,store和update(写入类操作)的费用远远高于其他
SMB-Tree(Suppressed Merkle B-tree)
与MB-Tree不同:只实现根节点而忽略中间节点(插入新对象时,同样要计算中间节点,但是只更新根节点值)
当插入一个新数据对象时:
智能合约将所有数据加载到内存中花费$N\cdot C_{sload}$
对这些数据进行排序,花费$N\log N\cdot C_{mem}$(NlogN是比较排序的最小时间复杂度)
计算hash值,需要计算$N/F$个hash值,花费$N/F\cdot C_{hash}$
写入新数据,修改根哈希值花费$C_{sstore}+C_{supdate}$
总的gas是
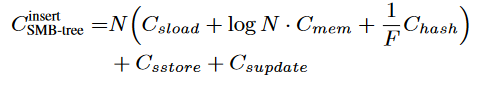
二者比较可以看出:
- 当N是一个比较小或中等的数时,SMB的花销小
- 当N很大时,SMB的花销超过MB
ADS设计需求
需要做到高效存储维护和查询:
- 避免维护过长的排序列表。随着数据库规模的增加,高的更新成本会削弱系统的性能。
- 使用更多的读操作而不是写操作。对于中间值,可以再内存中计算完之后再写入
- 适应不同规模的数据库。数据库规模会影响ADS的维护性能,理想的ADS应当能够适应不同大小的数据库
$GEM^2-Tree$
该ADS可以:
- 由智能合约进行维护,并且做到低gas
- 支持可验证查询
结构
由一颗完整的MB-Tree和一系列小的压缩的SMB-Tree组成,MB-Tree作为主索引,SMB-Tree作为新插入数据的索引。
这样做的好处:
- 将新数据插入小的SMB时,gas较少
- SMB中的数据可以批量合并到MB中,这么做可以节约更新成本
当有新数据插入时,SMB都需要进行重构,为了节约更新成本,将存储空间分为一组指数大小的分区,每个分区最多可以维护2个SMB,当插入数据变多时,SMB可以再合并。
分区是符合逻辑的,因为它们的大小会随着树的合并而变化
这种结构的优势:
- 新的数据总是被插入到较小的树中,这样可以将更新的代价最小化
- 对象写入存储后不需要重新排序,这是节约gas的关键
- 减小SP的维护代价:不需要在每个新数据到达时都进行重建
- 分区的总数为$O(\log N)$,这将有利于进行查询
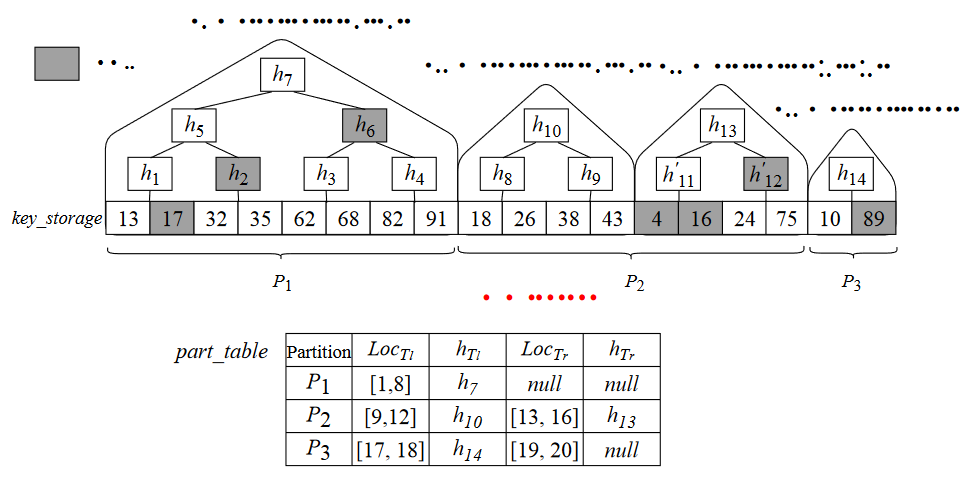
一个例子:
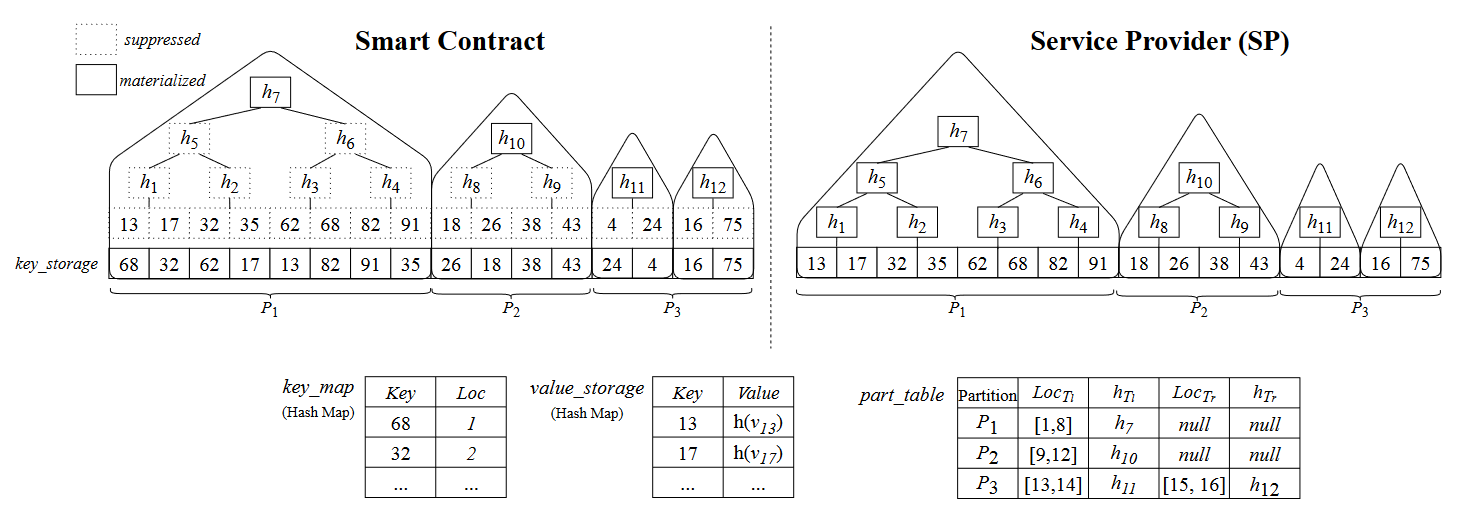
- 分区p1p2p3,一个分区包含一到两个树,表示为$T_{r}$和$T_l$
- part_table,针对分区的辅助索引,保存着存储位置范围、根哈希值,此处的根哈希值跟MB树上的稍有不同,因为SMB树中的根哈希值包含了key值的边界(例如,$h_7=h(13||91||h(h_5||h_6))$),用于查询时判断范围
- key_map,搜索键和存储地址的映射表,在数据更新时会用到,按照插入时的顺序排列
前两个是区块链和SP共有的,第三个只存于链上
链上的搜索键值是没有经过排序的,SMB在链上是压缩的,而在SP端由于需要查询所以是完整的
维护
三种操作:插入、更新、删除(可以看作更新为空数据)
MB树看作p0分区,由大到小SMB树包含有$P_1,…,P_{max}$,M为$P_{max}$(最小分区)中的树的大小的最大值
插入
新数据到来后:
首先到达$P_{max}$分区
- 如果分区未满,则插入到当前的树中
- 如果满了,则创建一棵含有新数据的SMB树,并把当前分区中已有的两棵树进行合并,进行下一步
将合并后的树放到$max-1$分区中
- 如果max-1分区中是空的,说明需要新建这个分区,此时将max的值加1
- 如果仍然是满的,需要再次将当前两棵树合并,继续放到之后的分区中
为了避免SMB树过大而造成高手续费(SMB树不适合数据过多时使用),设置一个SMB树的最大值$S_{max}$,如果需要合并的两棵树的大小超过了$\cfrac{S_{max}}{2}$,直接将它们插入到P0的MB树中
此处对于智能合约和SP有以下不同:
- 链上保存的是哈希值而不是原始数据
- 智能合约在此过程中会动态地创建SMB树(未排序且内部节点被省略)
更新
需要定位到更新对象的位置,然后更新根哈希值
- value_storage[key]更新哈希值H(value)
- 检查key_map,找到key的存储位置
- 找到保存该key值的分区
- 最简单的方式是查找part_table,但这种方式需要较高的手续费,因为可能需要遍历整个表
- 采取模数的方式,已知key的存储位置loc和分区最大值max,
- 如果不存在于SMB树中,则在MB树中
示例
可验证查询
查询过程
客户端发送查询请求Q=[lb,ub],SP返回查询结果和证明$VO_{sp}$
SP需要在MB和SMB树中进行搜索,然后把每棵树中的查询结果和验证对象合并起来
搜索过程如下:
- 首先在MB树中查找
- 如果查找范围与根节点中的范围不重合,说明这棵树中的数据不符合查询条件,则使用根哈希值和范围值作为VO
- 如果重合,则进行广度优先搜索。从根节点开始,如果非叶子节点符合查找范围则进一步查找,不符合则将节点哈希值和范围添加到VO中。到达叶节点时,SP将查询每个数据对象。属于查询范围的对象将被添加到查询结果中,而其他对象的hash将被附加到VO中
- 然后在SMB树左右子树中查找(同上)
验证过程
分两步
得到$VO_{chain}$
- 从链上获得GEM2Tree中所有树的根哈希值
结果验证(针对每一棵树)
- 正确性验证:重构根哈希值并和$VO_{chain}$比较
- 完整性验证:
- 当前树不符合查询:直接查看VO中给出的范围
- 当前树符合查询:检查边界搜索键来查询

