【强化学习】Policy-Gradient

简介

与Q Learning的比较

相比于之前学习的Q Learning，这个算法的不同点在于，可以不分析奖励值，直接从一个连续的动作空间中选择下一步要进行的动作，而Q Learning只能从有限多个动作中进行选择。

如何更新

Policy Gradients不使用反向传递误差来更新网络，而是使用环境给出的 reward 来进行反向传递，从而来决定是否增加这次选择的动作再次被选择的概率。

策略梯度如何下降

类比交叉熵

$$H(p,q)=-\sum_xp(x)\log q(x)$$

其中 $p(x)$ 为对应的标签，$q(x)$ 为输出的概率。

但在RL中是没有标签的。此时可以使用 reward 来充当标签。

假设一次状态行为序列为 $\gamma=\{s_1,a_1,r_1,s_2,…,s_t,a_t\}$ ，其中 $s_t$ 表示 t 时刻时的状态，$a_t$ 代表位于 $s_t$ 时采取的动作。这样的动作策略，使得我们得到了 reward $R(\gamma)$ 。接下来使用下面的式子进行计算：

$$L(\theta)=-\frac{1}{N}\sum_\gamma R(\gamma)\log\pi_\theta(\gamma)$$

其中 $\pi_\theta(\gamma)$ 表示了采取策略 $\gamma$ 的发生概率，N 为采样 $\gamma$ 的数目。

算法推导

算法中的策略梯度函数推导

将智能体的整个行为过程用数学表示如下：（表示成为一个动作和状态的序列）

$$p_\theta(\tau)=p_\theta(s_1,a_1,...,s_T,a_T)=p(s_1)\prod_{t=1}^T\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)$$

我们要优化的目标为：

$$\theta^*=arg\ \max_\theta E_{\tau\sim p_\theta(\tau)}[\sum r(s_t,a_t)]$$

即为遵循上面的状态、动作轨迹，所能达到的最大环境奖励值的期望，此时求得的策略就是最佳策略

这里进行如下的定义：

$$J(\theta)=E_{\tau\sim\pi_\theta(\tau)}[r(\tau)]=\int \pi_\theta(\tau)r(\tau)d\tau$$

其梯度如下：

$$\nabla_\theta J(\theta)=\int \nabla_\theta\pi_\theta(\tau)r(\tau)d\tau=\int \pi_\theta(\tau)\nabla_\theta \log \pi_\theta(\tau) r(\tau)d\tau$$

此处用到了一个定理：

这样的话就得到了下面的算式：

$$\tag{1} \nabla_\theta J(\theta)=E_{\tau\sim\pi_\theta(\tau)}[\nabla_\theta \log \pi_\theta(\tau) r(\tau)]$$

接下来专注求解 $\nabla_\theta \log \pi_\theta(\tau)$ 。将 $\pi_\theta$ 转换如下：

$$\pi_\theta(s_1,a_1,...,s_T,a_T)=p(s_1)\prod_{t=1}^T\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)\\ \log \pi_\theta(\tau)=\log p(s_1)+\sum^T_{t=1}\log \pi_\theta(a_t|s_t)+\log p(s_{t+1}|s_t,a_t)$$

在计算梯度时，由于第一项和最后一项均为常数（由环境本身决定），因此其梯度为0。最终将上式代入式 $(1)$ 可以得到：

$$\nabla_\theta J(\theta)=E_{\tau\sim\pi_\theta(\tau)}\left[\left(\sum ^T_{t=1}\nabla_\theta \log \pi_\theta(a_t|s_t)\right)\left(\sum^T_{t=1}r(s_t,a_t)\right)\right]$$

对策略梯度进行评估

经过前面的推导，我们可以得到如下公式：

这就是策略梯度的计算公式。可以利用如下的式子来更新当前策略：

$$\theta \leftarrow \theta+\alpha\nabla_{\theta}J(\theta)$$

接下来就可以初步的得到一个算法：

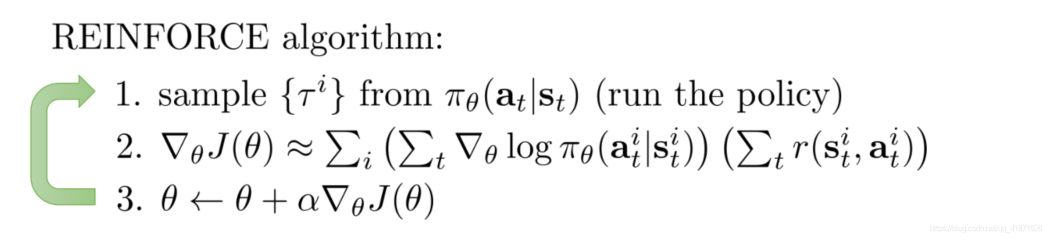
如何进行收敛

极大似然估计中的策略梯度如下所示：

可以看到，极大似然的公式和policy gradient只相差一个reward和的乘积。这样的话，在求解策略梯度时，就可以用求极大似然的方法来进行求解。

再观察策略梯度的公式：

$$\tag{2} \nabla_\theta J(\theta) \approx\frac{1}{N}\sum^N_{i=1}\nabla_\theta\log \pi_\theta(\tau_i)r(\tau_i)\\ =\frac{1}{N}\sum^N_{i=1}\left(\sum ^T_{t=1}\nabla_\theta \log \pi_\theta(a_{i,t}|o_{i,t})\right)\left(\sum^T_{t=1}r(s_{i,t},a_{i,t})\right)$$

式子中的梯度表明了增加轨迹 $\tau$ 概率的方向，可以看到式子中的 $\pi_\theta(\tau_i)$ 与奖励值相乘，这就表明如果奖励值大时，对应的高奖励的轨迹就更有可能出现，反之低奖励值的轨迹出现的概率更小。

部分观测时的算法设计

只需要将式 $(2)$ 中的 $s_t$ 修改成为 $o_t$ 即可，因为环境本身会直接给出奖励值，与观测多少数据是无关的。

Policy Gradient的高方差问题

高方差问题

策略梯度方法有一个重要的缺陷就是方差会很高。这里用一个简单例子进行说明，如下图：

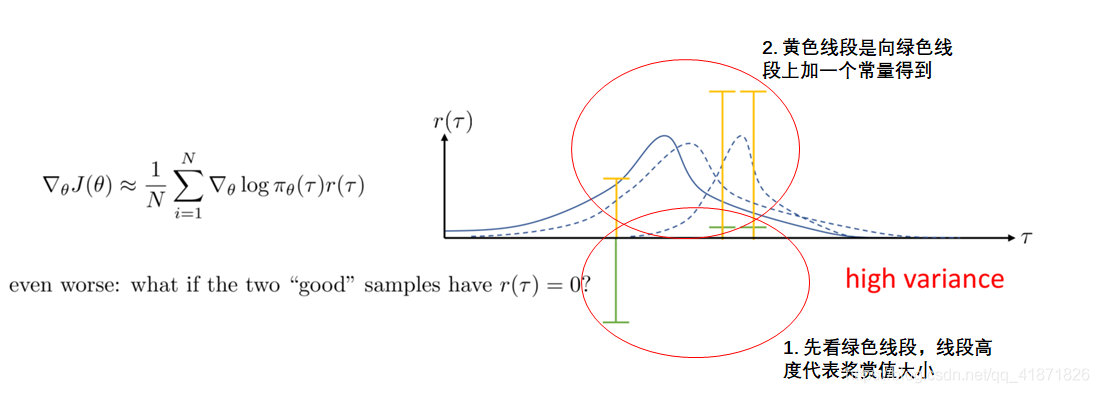
这里横坐标代表不同的采样样本，绿色线段是采样得到的智能体与环境交互后得到的奖赏值；第二步向第一步得到的奖赏值上加一个常量，该常量并不会影响策略梯度（下文也有相关推导）。但这两次得到的策略的概率分布结果却相差很多，这就是策略梯度方法高方差问题的直观体现，而高方差带来的问题就是算法更新的过程不稳定。

减小方差的方法

Causality假设

第一个是进行causality的假设：未来时刻的策略并不能影响之前时刻的奖赏值。

对原有的策略梯度公式中的奖赏值部分进行修改，原先的公式中后两项是先求和再相乘，如下：

$$\nabla_\theta J(\theta) \approx\frac{1}{N}\sum^N_{i=1}\left[\left(\sum ^T_{t=1}\nabla_\theta \log \pi_\theta(a_{i,t}|o_{i,t})\right)\left(\sum^T_{t=1}r(s_{i,t},a_{i,t})\right)\right]$$

修改之后的公式如下所示：只考虑从当前策略的时间往后推移的奖赏值，而不考虑之前的

$$\nabla_\theta J(\theta) \approx\frac{1}{N}\sum^N_{i=1}\left[\left(\sum ^T_{t=1}\nabla_\theta \log \pi_\theta(a_{i,t}|o_{i,t})\right)\left(\sum^T_{t=1}r(s_{i,t'},a_{i,t'})\right)\right]$$

加入Baseline

第二种方法在奖赏值的基础上减去一个常数(均值)，这个常数叫作baseline，公式化表示就是:

$$\nabla_\theta J(\theta)=E_{\tau\sim\pi_\theta(\tau)}[\nabla_\theta \log \pi_\theta(\tau) (r(\tau)-b)]$$

最简单的情况下取值为：

$$b=\frac{1}{N}\sum ^N_{i=1}r(\tau)$$

那么如何选择最优的baseline来最小化策略梯度本身的方差呢

方差计算公式：$Var[x] = E[x^2]-(E[x])^2$

将策略梯度的公式代入得到：

如果要使其最小，可以通过对其求导数并令其导数为0，从而求得最优的baseline的表达式，这里为了简化推导，令 $g(\tau)=\nabla_\theta\log p_\theta$

从而得到：

$$b=\cfrac{E[g(\tau)^2r(\tau)]}{E[g(\tau)^2]}$$

Policy Gradient方法的实现技巧

这里其实应当自己总结一下，不过先把课程中老师提到的技巧记录一下：

总体上只需要给出损失函数即可，剩下的任务交给tf或者pytorch去做

其他要点：

• 使用较大的batch size对参数进行更新
• 手动调整learning_rates很困难，可以使用ADAM优化器

Off-policy Policy Gradient

其实policy gradient的方法的高方差问题起源于该算法是on-policy的算法，由于每次采样必须使用新的策略，所以每次采样的数据在一次梯度上升之后就被扔掉了。

有一种解决方法是使用 importance sampling：